 Apparently Benoît Mandelbrot passed away last week. He is famous for introducing the world to the idea of “fractals” — shapes that are so crinkly that their boundaries are not lovely smooth lines or planes, so that their dimensions are not whole numbers — and the “Mandelbrot set” — that famous heart-shaped blobby thing with circular blobs stuck to it — although it should be noted that many of the ideas had been around for quite a while before Mandelbrot. However, his thinking coincided with the development of more accessible computing power capable of graphical representations, and the Mandelbrot set sort of became the geek psychedelia of the 1970s and 1980s.
Apparently Benoît Mandelbrot passed away last week. He is famous for introducing the world to the idea of “fractals” — shapes that are so crinkly that their boundaries are not lovely smooth lines or planes, so that their dimensions are not whole numbers — and the “Mandelbrot set” — that famous heart-shaped blobby thing with circular blobs stuck to it — although it should be noted that many of the ideas had been around for quite a while before Mandelbrot. However, his thinking coincided with the development of more accessible computing power capable of graphical representations, and the Mandelbrot set sort of became the geek psychedelia of the 1970s and 1980s.
I came across the ideas in the mid to late 1980s, at the same time as getting my first computer. I programmed my 64K Amstrad to produce my own images of the Mandelbrot set. I chose to do it in four glorious colours, which was my compromise — forced on me by the Amstrad’s graphics limitations — between not having the image too pixellated and at least having some psychedelia (which is ironic, because the Mandelbrot set is actually the “boring” black bit!). I could zoom in manually, blithely paying no attention to whether or not the computer could handle the number of decimal places I was demanding of it, and at one stage the program ran for three days because the calculations took that long (my current computer will do the same thing in the tiniest fraction of a second), and all the time I was worried whether or not there would be room on the 160kB external disk to store the file.
[21 Nov update: I managed to find the slide photos I took of some of the Amstrad’s Mandelbrot set images back in the 1980s. By an amazing fluke, it seems that the two images I happen to have here are of the same region. As you can see, the Amstrad’s output is rather coarse and primitive compared to the Mac’s contemporary effort, but at the time it was pretty remarkable … not least because I’d done the programming myself.]
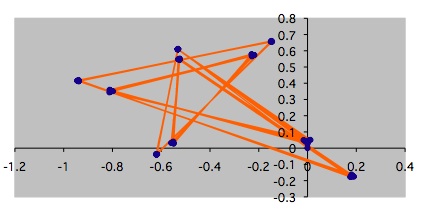
Over the years I have come to learn a few more things about the Mandelbrot set, including the really nice relationship between the different blobs and what happens to the points within the blobs when you apply the special iteration formula that underlies the whole process. Some of the points spiral in and converge to a single point, as shown in the first image below. Other points bounce around for a bit and then settle down to oscillate between several points, as shown in the second image below (there are 10 points in the final cycle, and the iteration just keeps visiting them over and over again). That second image used a point from the biggest full circle shown in the picture above. The cool thing is that every point you choose to iterate from that particular circle will settle down to a 10 cycle. On the other hand, if you pick points from one of the other blobby bits, then they will settle down to a cycle of a different length … but all the points within your chosen blob will have the same length of cycle. And there are really cool relationships between the lengths of the cycles and where the blobs are on the Mandelbrot set.
Anyway, the full explanation is a bit too long for a blog entry, but it is awesomely froopy stuff and I’ve spent a goodly portion of my adult life playing with it.
Vale Mandelbrot.
 Helen Chick
Helen Chick


It’s a bit irreverent sorry, but I read someone comment that the police were glad the death was not suspicious, because it would have taken days to draw the chalk outline.
ROTFL. Love it.
Being a bear of very little brain (and even littler mathematical brain) I can’t understand why fractals etc are beautiful – but I can appreciate the whorls and swoops and the sheer wonder of the results.
I can remember you trying to explain the Mandelbrot thingy to me eons ago. It had something to do with running around the coastline of Tasmania with a ball of string! Colin’s graphic example is much more fascinating!