A personal mathematical history – Part 2

[Note: This four-part series is a blogged version of a talk I gave in 2011 at a conference which celebrated the 50th anniversary of the Mathematical Association of Tasmania. Some of the anecdotes shared here were not included in the original talk … and, given that I’m writing this up over three years later, I’m quite sure there were bits included in the talk that are missing from this version of things.]

The mid to late 1970s saw me at high school. There was a hint that maths might become a key interest for me when, in Grade 7, I tried to find out the formula for the circumference of an ellipse. However, I could barely draw one let alone measure its circumference accurately (I didn’t learn about the nice construction shown in the second diagram until I took an elective on technical drawing in Year 11 or 12, technical drawing not having been part of a girl’s high school curriculum during my schooling). I think I had vague ideas of experimenting with π (pi) and “length” and “width” to see if I could come up with a formula, but given that my poorly drawn ellipses were never measured accurately I soon realised this was a lost cause. In the absence of Google I couldn’t look it up quite as easily as I can now, and my maths teacher, though intrigued by my interest, didn’t know the answer either. In fact, there is no nice easy answer: area is a nice and simple π x length x width, but circumference is a whole lot more complicated.

There was also a hint, in grade 8, that I was/am no mathematical genius at all. Negative numbers and I are now very good friends, with that comfortable take-it-for-granted familiarity that comes with time and greater understanding … but back in Grade 8 I didn’t do very well on the test (nor did anyone else). They are tricky things to teach — if you want to do better than merely drumming in mindless rules — because there is no good set of materials that model all the operations (what works for addition doesn’t work very well for multiplication, for example).

The 1970s also saw the coming of the affordable pocket calculator (where “affordable” still meant a sizeable portion of one’s pocket money: the four-function calculator shown below — my first — cost me $10 which was a lot of money back then; and Dad’s first scientific calculator was $100 if I recall correctly). My first calculator had an interesting quirk which makes it an important possession. It has no square root button nor memory capacity (features typical of  current “four function” calculators), and has only a 6 digit display, although it can actually show 12 digits with the use of the arrow key, thus allowing you to get a complete answer for the product of two 6-digit numbers (something most four function calculators couldn’t do, as they would get an overflow error). The really quirky thing, however, is associated with the fact that it does not give an error message in the classic situation of “dividing by 0”. Dividing by 0 is an undefined operation in mathematics, and if you ask this Casio calculator to work out something like 6÷0 it actually starts counting like a stopwatch, as if it is trying to count how many 0s go into 6.

In Year 9 we got to choose certain optional subjects and I chose advanced maths. If memory serves, this might have been the first year that scientific calculators were allowed into classrooms (though not into exams, of course!). I had a TI-30, and the first problem was to find the “on” switch, because up until then there was a definite separate switch on the side of the calculator, rather than an “on” button in amongst all the other buttons. These machines took 9V batteries, and were only accurate to the displayed number of decimal places (most calculators since have a few extra hidden digits for greater accuracy). Later calculators would be able to do numerical integration, be programmed, and eventually do symbolic algebra and calculus (and I do recall, with some amusement, the calculator of one of my uni friends which was robust enough to survive repeated defenestration from the third storey of the physics building at the University of Tasmania).

As suggested above, we could use calculators in class, but not in exams, which meant that we still had to learn how to use mathematical tables to find logarithms and trigonometric ratios. Their demise in the following years has rendered the following mathematical joke largely incomprehensible: Noah, on sending all the animals out from the ark after the flood with a command to go forth and reproduce, is disappointed to come across two snakes sitting around still doing nothing, and so he chops down a tree and builds a rough platform for them, places them on it, and soon thereafter hears the slither slather of little tiny scales … because the snakes were adders and adders need log tables to multiply.

As an aside, Benford’s law was identified from the fact that the most dog-eared pages of a set of log tables were those associated with the numbers starting with the digit 1, revealing that a larger proportion of the numbers that arise in (certain aspects of) everyday life are those that start with a 1, while fewer start with 2, fewer still with 3, and so on. If you were to go into, say, KMart and note the prices of things, you’d find a bunch of things in the $10-$19 range, some in the $20-$29 range, fewer in the $30-$39 range, and so on, and then there’d be a jump again when you get to the things in the $100-$199 range with more in this range than in the $200-$299 range (this may not be totally true for KMart on its own, but it is truer across a collection of stores). It has been possible to detect tax fraud because people have used random numbers for their entries, when, in fact, the sorts of numbers that are more likely to appear on a tax return will follow Benford’s law, with a higher proportion of numbers starting with the digit 1.

One of the famous mathematical things to happen in the 1970s was the proof of the famous Four Colour Theorem. This result — that any map of regions can be coloured in with just four colours at most — had long been thought to be true but earlier attempts to prove it had been inadequate. What was remarkable — and, for mathematicians, disconcerting — about the 1976 proof was that it was done largely by a computer, which was used to evaluate the large number of possible cases that have to be considered. This made the proof, in some sense, uncheckable by human reasoning and raised questions about what constitutes a valid mathematical proof.

My high school mathematics classroom was fairly typical of the day, with the teacher explaining stuff and showing us how to “do” the problems, but we did escape into the outdoors on at least one occasion and actually measured the slope of a real-world street.

Our trigonometry problems were pretty standard textbook fare with angles of elevation and the like, but some years later one of my brothers posed a nice real-life trigonometry problem from a bushwalking trip that he did. I use this problem with my pre-service teachers; not all of my students use trignometry directly to solve it (although it is usually implicit in the solution approach).

One of things that has changed since my high school days is the amount of geometry and proof included in the high school curriculum. We did quite a lot and I enjoyed the process of puzzling out the relationships that would yield the desired results, and although nobody did any Latin there was something very satisfying about writing QED at the end of a proof. This enjoyment of proof – or, at least, proofs of a certain deductive kind — has been a significant factor in my journey as a mathsy person.

One of the key things that happened in our advanced maths class was that we discovered certain of the Pythagorean triples for ourselves. We could see the patterns that were there, but couldn’t actually come up with a proof for ourselves at the time. The air of discovery and intrigue was very exciting for me: there were patterns out there waiting to be discovered, and, if you could only figure out how, verified. This was a telling experience for me; my Year 11 maths teacher later provided me with the proof of the result (this experience is further recounted in a conference paper I wrote which you can download here).

Problem solving was a formal part of my high school experience as well. The influence of Georg Polya’s How to Solve It had reached Tasmanian classrooms, and in Year 8 we had a formal block of problem solving experiences. I’m not sure that it was particularly well integrated into the rest of our more traditional routine learning, but at least we got to meet some nice problems and problem solving strategies.

The four fours problem — in which the object is to use only and exactly four copies of the digit 4 and any operations you like to create the numbers 1 to … well, it was 100 for us — is one of my favourite problems. It is so tightly constrained that it seems almost impossible, but working on the task provides an opportunity to get to know numbers and their relationships really well. It has always seemed ironic to me that my list of solutions for the numbers 1 to 100 is missing four numbers. There’s a part of me that would like to go back and fill these gaps (in fact, there is a solution that covers every whole number, but I don’t remember it and I stubbornly refuse to look it up again!), and there’s a part of me that thinks missing four is entirely apt.

Problem solving had its climax in the annual competitions. I used to do reasonably well on the ones with short straightforward questions but not so well on the tougher questions. There is a particularly irony that arises from the following slide: the M L Urquhart paper was the peak Tasmanian problem solving paper for Year 12 maths students (M L Urquhart being one of the founders of the MAT). I sat the paper in 1981 and certainly didn’t win; in fact, I suspect I answered only a few bits of the questions and looking at it now I suspect that some of the questions will be beyond the reach of most current year 12 students, not least because the notation is likely to challenge them. The reason I am a little aware of the capacity of current year 12 students is that this year I was the one who actually set the 2014 M L Urquhart paper.

The next slide shows the textbook du jour for one of my Year 12 advanced maths subjects (there were two such subjects and I did both, so it is probably safe to say that my mathematical path was now more obvious). This textbook was a collection of exercises; there was also an accompanying guide with model solutions for some problems, and both of them were characterised by their monochrome down-the-line mathsiness: no colour, no photos, few diagrams, just lots of problems to do.

There was, however, one interesting challenge that we were set by one of our teachers. He gave us two sheets of identical grid paper, and promised to take us out to dinner at a top restaurant if we could find a way to place one sheet above the other so that there was no point on the top sheet that was directly above the exact same point on the flat bottom sheet. We could fold or crumple — but not tear — the top sheet as much as we liked. Helen-the-gullible took him at his word, thinking that this was an achievable task (even though she knew that proving that something does not happen can be harder than proving that something does). What she didn’t know — and couldn’t have at the time, since the necessary maths would not be met until university — is that there is a “fixed point theorem” that says there’ll always be at least one point that lines up.

The fixed point theorem is kind of technical in the way it is stated, although it can be visualised fairly easily. For one dimension the technical version says that if a function f is continuous on the interval [a, b] and f(x) always takes its values between a and b then there exists a point c where f(c) = c (i.e., if you plug in c you get c back out). This is more easily visualised and explained by the following diagram. Imagine that you have to start anywhere on the left hand border of the square below and finish up on the right hand border, and that you have to draw a squiggly line with no breaks (this is basically what continuous means). Whatever you draw (e.g., the red line below), now matter how hard you try, simply cannot avoid crossing the blue line. The place where the two cross is the “fixed point”. For the paper example above, which is a two dimensional version of the fixed point situation, our crumpled up piece of paper is like the red line (the “no tearing” means that the function is continuous), and the grid paper underneath is the equivalent of the blue line — and the fixed point theorem says that somewhere on that grid there’ll be a place where a point lines up exactly (just as there’ll be somewhere where the red and blue lines have to cross; they can’t avoid it). 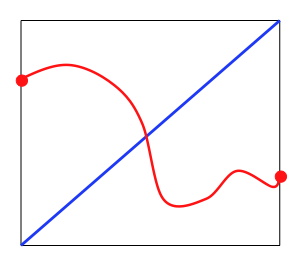So, nobody got a free dinner. Our teacher knew he was safe. 🙂