[Note: This four-part series is a blogged version of a talk I gave in 2011 at a conference which celebrated the 50th anniversary of the Mathematical Association of Tasmania. Some of the anecdotes shared here were not included in the original talk … and, given that I’m writing this up over three years later, I’m quite sure there were bits included in the talk that are missing from this version of things.]
In the course of my mathematical education I have learned some pretty cool things (well, I think they’re cool; your mileage may vary). Learning more about irrational numbers — numbers that have a decimal expansion that goes on forever without repeating — was amazing, especially the idea that there are more of these numbers than there are fraction-type numbers (I’m planning on doing a blog post about this one day; I was going to do it in the MAT talk, but I didn’t have time so I omitted it then as well). Pi is such a number, and I have in my possession a windcheater with some of the digits of pi printed in varying degrees of boldness so that the symbol ? is visible from the mass of digits.
Here is a closeup view; you can see the famous first few digits 3.1415926535… . What you can’t see in that closeup is the string of six 9s that occurs within the first 1000 digits of pi.
One day I went looking for the string of six 9s (the image below shows that it really is there), and I found it on my windcheater as expected. I then went looking for it to show an at-least-as-geeky friend … and found the six 9s in an entirely different location. I knew it’s extremely unlikely that there would be two such strings, and so I examined my windcheater closely and realised what the manufacturers had done. Instead of showing the first 20000 digits of pi, they had copied and pasted just the first thousand or so digits over and over again. Not only does the windcheater show a terminating decimal, but it’s a repeating decimal as well — both of the things that pi very definitely is not! At first I was disappointed but then I realised that I had a great teaching tool for highlighting exactly what pi is supposed to be like.
The irrational numbers are, in some sense, “ugly” because they can’t be written as nice fractions (this is, in fact, their very definition). Some interesting things can be discovered in maths if you start asking what happens when we “do” things to different kinds of numbers. Raising something to an irrational power seems like a pretty “ugly” thing to do (raising something to a whole number power, e.g., squaring and cubing, is nice and easy; raising something to the power of pi, or some other irrational, actually seems vaguely incomprehensible if you think about it too much). So, an interesting question arises: if you raise an irrational to the power of irrational (an ugly to the power of an ugly!!) then could it turn out to be a “nice” number like a simple fraction (or “rational” number)? (The definition of a rational number is a number that can be written as a fraction, or in other words as a whole number divided by another whole number, give or take a negative sign).
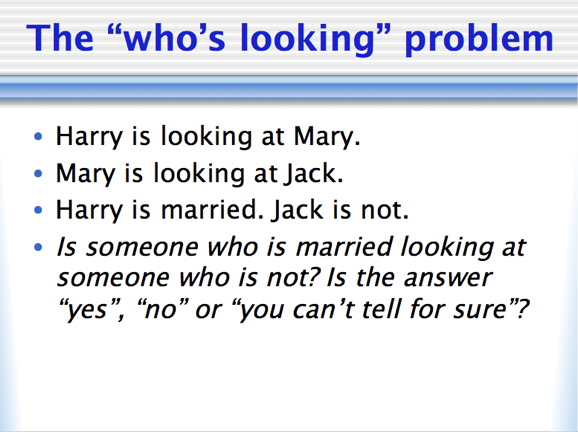
Before we answer this, I want to give you another problem. In fact, I’d put this on display right at the beginning of my talk. Before you read any further, I want you to try answering it.
No, you can’t read any further unless you have an answer!
Alright, keep that in the back of your mind for now and we’ll turn back to the question about raising an irrational number to the power of an irrational number. Is it possible that the result could be a nice rational number? It is very important to realise that there are only these two types of (real) numbers: either a number is rational (i.e., it can be written as a fraction, which means it will either make a terminating decimal like 2/5 = 0.4 or a repeating decimal like 4/11 = 0.36363636… ) or it is irrational (i.e., it’s a number like pi = ? = 3.1415926… or ?2 = 1.4142…, which can’t be written as a fraction and which is a non-terminating non-repeating decimal).
Let’s take ?2 as an example of an irrational number. Now consider the number ?2?2 which is obviously an example of an irrational number raised to the power of an irrational number. Now, I have no idea what the answer is! However, it can only be one of two things, because there are only two types of number. So, as one alternative, it could be rational.
If it is rational, then we’re done, because we found an example of an irrational to the power of an irrational being rational.
On the other hand, the second alternative is that it is irrational.
Well, if ?2?2 is irrational, then if we take this to the power of ?2, i.e., (?2?2)?2 then this is an irrational (?2?2) being raised to an irrational power (?2).
But if you remember your index laws, you will know that (?2?2)?2 =?2?2x?2 = ?22 = 2, and since 2 is a nice lovely rational number (it’s a terminating decimal or the fraction 2/1), we’ve just found an example of an irrational to the power of an irrational being rational.
So, one way or the other, we have that an irrational to the power of an irrational can be rational. Ironically we don’t know which one is the one that is rational, only that one or other of them must be and so there exists an example (this is what is known as an “existence proof”: it shows us that something exists but doesn’t tell us where to find it).
Now, the cool thing about the proof about irrational powers is that solving the “who is looking at who” problem has exactly the same structure. We don’t know Mary’s marital status, but she has exactly two options: she is either married or not. If she isn’t then the married Harry is looking at the unmarried Mary; if she is married, then she is married and looking at the unmarried Jack. Either way, somebody who is married is looking at somebody who is not, even though we don’t know which case actually applies.
If you look at the slide above and the slide below, you can see that the structures of the arguments are the same. This is what is known in maths as an isomorphism. Isomorphisms are cool, because if you know something about one situation then you know the same things for all isomorphic copies of that situation. A lot of my PhD thesis was tied up with isomorphisms. [I have blogged about these two arguments on another occasion; I apologise for the repetition but it was in the talk and it fits the structure of what I want to say.]
As mentioned in Part 3, at the end of my PhD I could tell that my future might not lie solely in mathematics for mathematics’ sake, and before long I had moved full-time into Maths Education (which had had some of my attention as a parallel interest while I worked and studied my PhD). In this area I have learned more about the teaching and learning of mathematics of all levels of schooling. At the time of giving the MAT anniversary talk I was working at the University of Melbourne, although by the beginning of the following year I had returned to the University of Tasmania but to the Faculty of Education instead of the maths department.
Although I had covered a range of mathematical ideas, there were quite a few mathematical results that take my fancy but which time constraints had precluded from the talk. That’s the thing about maths: there really are some beautiful amazing paradoxical things that are kind of fun to know about.
It seemed highly appropriate to conclude with a thank you to those who had been part of my mathematical journey, who had influenced and inspired me and introduced me to some of the awesome ideas.
 Primary school teacher: Mr Taylor (more into science than maths, but certainly built interest in the sciences)
Primary school teacher: Mr Taylor (more into science than maths, but certainly built interest in the sciences)
High school teachers: Mrs Edwards, Bill Heap, Ian Smith (advanced maths teacher in grades 9 and 10 and particularly influential)
Senior secondary college teachers: Martin Lowry (showed me the proof about the Pythagorean triples), Norm Gregory (offered the fixed point theorem dinner reward), Ken Walsh (offered a technical drawing elective which I loved).
Undergraduate lecturers and later colleagues: Bruce Brown, John Donaldson, Prof Elliott, Barry Gardner, Des Fearnley-Sander, David Paget, Don Row, Jane Watson, Robyn Gregory.
Honours and PhD supervisor: Barry Gardner
Mentor in maths education and general encourager: Jane Watson
Fellow undergraduate and postgraduate students: Kim Beswick, Tim Stokes, Nick McConnell.
Other colleagues and fellow teachers and mathematical inspirers: Neville Windsor (my birthday twin), John Dowsey, Kaye Stacey, Anne Watson, John Mason, Ken Milton (DipEd maths lecturer), Howard Reeves
Authors: Ian Stewart, John Horton Conway, George Polya; Stocks, Morris, Buckley and Leo (HSC textbook authors)
 Helen Chick
Helen Chick













Wonderful reading Helen! I like to think you cut your maths teaching teeth on me in Advanced Maths – I’d never have passed if I hadn’t sat next to you. Lovely seeing the old logarithm book and calculator too. I remember filling the inside of my folder with quotes from Smithy & the class like ‘well 2 minus 0 should equal 0″.
I have very fond memories of those advanced maths days. (And I’m fairly sure you held your own well enough if I remember rightly.)