 Some of you may be familiar with the so-called “Platonic solids”, which are the five “regular” solids in three-dimensions. “Regular” means that they are made up of flat shapes that are “regular” in the sense of having sides of equal length and angles that are all equal, and then these flat shapes are stuck together to make up a solid, and, in addition, every vertex (pointy corner) of the given solid always has the same number of flat shapes meeting at it.
Some of you may be familiar with the so-called “Platonic solids”, which are the five “regular” solids in three-dimensions. “Regular” means that they are made up of flat shapes that are “regular” in the sense of having sides of equal length and angles that are all equal, and then these flat shapes are stuck together to make up a solid, and, in addition, every vertex (pointy corner) of the given solid always has the same number of flat shapes meeting at it.
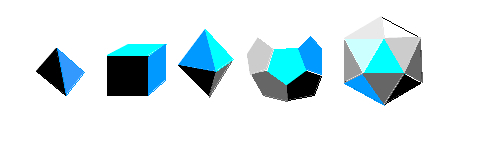
Pictures of the five Platonic solids are shown at right: the tetrahedron (a special triangular-based pyramid where all four sides are nice equilateral triangles), the cube (six squares, the square being the quadrilateral that is regular), the octahedron (eight equilateral triangles, and there are always four of these meeting at each vertex), the dodecahedron (12 regular pentagons, with always three meeting at a vertex), and finally the icosahedron (20 equilateral triangles, and every vertex has five such triangles meeting at it). These are the only five such shapes that exist in our well-known three-dimensional space, a fact that was known to the ancient Greeks.
 If you can accept the idea of four spatial dimensions (see very brief and inadequate explanation at the end of this post) then we can ask the question “What are the equivalents of the Platonic solids in 4D?”, or, in other words, what are the 4D shapes that are made up of regular 3D solids (just as 3D shapes are made up of 2D ones).
If you can accept the idea of four spatial dimensions (see very brief and inadequate explanation at the end of this post) then we can ask the question “What are the equivalents of the Platonic solids in 4D?”, or, in other words, what are the 4D shapes that are made up of regular 3D solids (just as 3D shapes are made up of 2D ones).
The answer is — sort of — at right (the thing in the middle is an Australian $1 coin, which is 2.5cm/1 inch in diameter). There are 6 regular convex polytopes in four dimensions, and thanks to the generosity of my Melbourne work friends I now have a set of 3D representations of them, given to me as a farewell gift. They are amazingly beautiful and mindblowingly fun to think about. Of course, the things I have (more photos are here) are NOT actual 4D objects but 3D depictions of 4D objects. Think about what happens when you draw a cube on paper: the drawing is two-dimensional — it’s on flat paper — even though the original cube that you are trying to depict is three-dimensional. What happens in the drawing is that you “cheat” a bit and draw some of the lines at slanty angles to represent the depth or third dimension. In other words, you lose a dimension in the drawing, but it “gets away with it” by drawing some of the right angles as slanty lines. My set of polytopes does the same thing: the shapes in the photo are 3D “pictures” of real 4D objects (if we could perceive 4D), but because we’re stuck in 3D we’ve lost one of the dimensions, and some of the lines have to be represented wonkily instead of at the angles that they “really” are in four dimensions.
[Strictly speaking the shapes in the photograph itself are actually 2D representations (since the photo is flat) of the 3D shapes which I have and which were sitting on my floor for the photo, and these 3D shapes are, in turn, representations of the 4D objects which I don’t have and can only vaguely imagine!! Anyone who isn’t confused at this point isn’t paying attention.]
Closeup photos of each of the shapes, and some accompanying explanation (of dubious lucidity) can be found here.
* * * * * * *
Very brief discussion about 4D
“Four dimensions” just means that there are four variables involved. Most people, if they think about 4D at all (you mean people don’t?!), probably know of 4D as “space-time” (the famous “space-time continuum ” of science fiction … and reality!). This is three dimensional space and time. Space-time thus has four variables: left-right, up-down, towards-awayfrom, and time, and any “point” in space-time can be defined in terms of four coordinates: where you are (which takes three coordinates) and when you are (which is an extra coordinate). (This assumes that we all agree on points of reference for the origin point of space and the start of time!).
But these are not the only sets of four variables that we could have. 4D space also has four variables: left-right, up-down, towards-awayfrom, and an extra, fourth, direction which is at right angles to each of the first three (which we don’t experience as far as we know, but you could think of it as going off in a wonky direction, just like the slanty lines of a cube in a 2D drawing that tries to show 3D on a flat piece of paper). It takes four coordinates (w,x,y,z) to describe where something is in 4D space (just like 2D geometry has (x,y) coordinates, and 3D geometry has (x,y,z) coordinates). Now this might seem totally unrealistic to you, because we don’t perceive that fourth right angle (well, I don’t; I can’t speak for the rest of you), but there are actually plenty of real-life situations that involve multiple variables, that we might like to graph (just as we draw graphs of distance as a function of time to show how something is travelling). So, for example, heights of plants might depend on four variables: amountofwater, amountofsunlight, amountoffertiliser, and amountoftalkingtobyowner. We might even be able to get a formula to describe how all these things interact, but what we really struggle with — BECAUSE we don’t perceive the fourth dimension — is being able to draw graphs of these relationships because we can’t easily show all four (or five or six or seven …) of the variables/coordinates.
For a fun and famous book about the difficulties of making sense of “moving up” a dimension, try Flatland, by Edwin A Abbott, which describes the adventures of a square living in a flat 2D world, who suddenly starts to experience the third dimension.
 Helen Chick
Helen Chick
I ran across an excerpt from Flatland when I was growing up, and then when I saw that my seventh-grade math teacher had a copy of the book, I asked her if I could borrow it. I remember she was surprised that I wanted to read it. I downloaded it for my Kindle but haven’t re-read it yet. I do remember enjoying it.
[…] have written more about the fourth dimension previously and I also have photos of some other 4D shapes with extra explanations if you’re interested […]